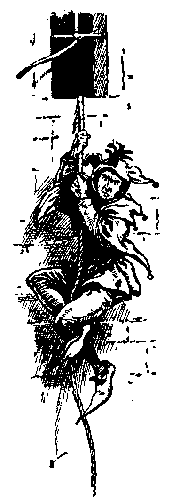The Banner Puzzle.
A Lady had a square piece of bunting with two lions on it, of which the
illustration is an exactly reproduced reduction. She wished to cut the
stuff into pieces that would fit together and form two square banne...
|
The Industrious Bookworm.
Our friend Professor Rackbrane is seen in the illustration to be
propounding another of his little posers. He is explaining that since he
last had occasion to take down those three volumes of a learned book
fro...
|
A New Money Puzzle.
The largest sum of money that can be written in pounds, shillings,
pence, and farthings, using each of the nine digits once and only once,
is L98,765, 4s. 31/2d. Now, try to discover the smallest sum of money
t...
|
The Barrels Of Balsam.
A merchant of Bagdad had ten barrels of precious balsam for sale. They
were numbered, and were arranged in two rows, one on top of the other,
as shown in the picture. The smaller the number on the barrel, the
g...
|
The Ten Apples.
The family represented in the illustration are amusing themselves with
this little puzzle, which is not very difficult but quite interesting.
They have, it will be seen, placed sixteen plates on the table in th...
|
The Grand Lama's Problem.
Once upon a time there was a Grand Lama who had a chessboard made of
pure gold, magnificently engraved, and, of course, of great value. Every
year a tournament was held at Lhassa among the priests, and whenever...
|
The Mysterious Rope
My dungeon did not lie beneath the moat, but was in one of the most high parts of the castle. So stout was th...
|
A Packing Puzzle.
As we all know by experience, considerable ingenuity is often required
in packing articles into a box if space is not to be unduly wasted. A
man once told me that he had a large number of iron balls, all exactl...
|
A Shopping Perplexity.
Two ladies went into a shop where, through some curious eccentricity, no
change was given, and made purchases amounting together to less than
five shillings. "Do you know," said one lady, "I find I shall requir...
|
Heads Or Tails.
Crooks, an inveterate gambler, at Goodwood recently said to a friend,
"I'll bet you half the money in my pocket on the toss of a coin--heads I
win, tails I lose." The coin was tossed and the money handed over. ...
|
The Abbot's Puzzle.
The first English puzzlist whose name has come down to us was a
Yorkshireman--no other than Alcuin, Abbot of Canterbury (A.D. 735-804).
Here is a little puzzle from his works, which is at least interesting on
a...
|
Boards With An Odd Number Of Squares.
We will here consider the question of those boards that contain an odd
number of squares. We will suppose that the central square is first cut
out, so as to leave an even number of squares for division. Now, it...
|
More Mixed Fractions.
When I first published my solution to the last puzzle, I was led to
attempt the expression of all numbers in turn up to 100 by a mixed
fraction containing all the nine digits. Here are twelve numbers for the
re...
|
What Was The Time?
"I say, Rackbrane, what is the time?" an acquaintance asked our friend
the professor the other day. The answer was certainly curious.
"If you add one quarter of the time from noon till now to half the time
from...
|
The Junior Clerk's Puzzle.
Two youths, bearing the pleasant names of Moggs and Snoggs, were
employed as junior clerks by a merchant in Mincing Lane. They were both
engaged at the same salary--that is, commencing at the rate of L50 a
year...
|
The Haberdasher's Puzzle
Many attempts were made to induce the Haberdasher, who was of the party, to propound a puzzle of some kind, b...
|
The Ball Problem.
A stonemason was engaged the other day in cutting out a round ball for
the purpose of some architectural decoration, when a smart schoolboy
came upon the scene.
"Look here," said the mason, "you seem to be a sh...
|
Average Speed.
In a recent motor ride it was found that we had gone at the rate of ten
miles an hour, but we did the return journey over the same route, owing
to the roads being more clear of traffic, at fifteen miles an hour...
|
Bishops In Convocation.
[Illustration:
+---+---+---+---+---+---+---+---+
| B | B | B | B | B | B | B | B |
+---+---+---+---+---+---+---+---+
| | | | | | | | |
+---+---+---+---+---+---+---+---+
|...
|
The Greyhound Puzzle.
In this puzzle the twenty kennels do not communicate with one another by
doors, but are divided off by a low wall. The solitary occupant is the
greyhound which lives in the kennel in the top left-hand corner. W...
|
 Informational
Informational