A DORMITORY PUZZLE.
(
Combination and Group Problems)
In a certain convent there were eight large dormitories on one floor,
approached by a spiral staircase in the centre, as shown in our plan. On
an inspection one Monday by the abbess it was found that the south
aspect was so much preferred that six times as many nuns slept on the
south side as on each of the other three sides. She objected to this
overcrowding, and ordered that it should be reduced. On Tuesday she
found that five times as many slept on the south side as on each of the
other sides. Again she complained. On Wednesday she found four times as
many on the south side, on Thursday three times as many, and on Friday
twice as many. Urging the nuns to further efforts, she was pleased to
find on Saturday that an equal number slept on each of the four sides of
the house. What is the smallest number of nuns there could have been,
and how might they have arranged themselves on each of the six nights?
No room may ever be unoccupied.
[Illustration
+---+---+---+
| | | |
| | | |
| | | |
+---+---+---+
| ||/| |
| |--| |
| |/|| |
+---+---+---+
| | | |
| | | |
| | | |
+---+---+---+
]
Read Answer
Next:
THE BARRELS OF BALSAM.
Previous:
COUNTER CROSSES.
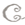Canadian Stories - Download the EBook French Canadian Stories
Informational
