Ovid's Game
(
MISCELLANEOUS PUZZLES)
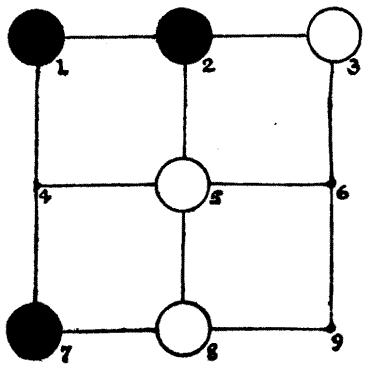
Having examined "Noughts and Crosses," we will now consider an extension of the game that is distinctly mentioned in the works of Ovid. It is, in fact, the parent of "Nine Men's Morris," referred to by Shakespeare in A Midsummer Night's Dream (Act ii., Scene 2). Each player has three counters, which they play alternately on to the nine points shown in the diagram, with the object of getting three in a line and so winning. But after the six counters are played they then proceed to move (always to an adjacent unoccupied point) with the same object. In the example below White played first, and Black has just played on point 7. It is now White's move, and he will undoubtedly play from 8 to 9, and then, whatever Black may do, he will continue with 5 to 6, and so win. That is the simple game. Now, if both players are equally perfect at the game what should happen? Should the first player always win? Or should the second player win? Or should every game be a draw? One only of these things should always occur. Which is it?
Read Answer
Next:
The Farmer's Oxen
Previous:
Noughts And Crosses
Free Jokes.ca - Download the EBook Stories Jokes
Informational
